【理論】平成28年 問6|直流電源を加えた抵抗の直並列回路における電流比の計算問題
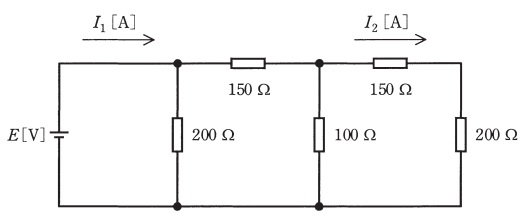
図のような抵抗の直並列回路に直流電圧 \( E = 5 \) [V] を加えたとき,電流比 \( \displaystyle \frac{I_{2}}{I_{1}} \) の値として,最も近いものを次の (1)~(5) のうちから一つ選べ。
合格への方程式
キルヒホッフの法則
キルヒホッフの法則は電気回路の基本的な法則で、電流と電圧の関係を表します。この法則は「キルヒホッフの電流則(KCL)」と「キルヒホッフの電圧則(KVL)」の2つから成ります。
任意の節点(接続点)において、流入する電流の総和は流出する電流の総和に等しい。
\[ \begin{aligned} \sum_{k} I_k = 0 \\[10pt] \end{aligned} \]
これは「電荷保存の法則」を意味し、節点に電荷が溜まらないという物理的な事実に基づいています。
閉回路(ループ)において、電圧降下の総和はゼロである。
\[ \begin{aligned} \sum_{k} V_k = 0 \\[10pt] \end{aligned} \]
これは「エネルギー保存の法則」を意味し、閉回路を一周したときにエネルギー変化の総和がゼロになることを表しています。
例題:キルヒホッフの電流則の適用
下図の節点Aにおいて、キルヒホッフの電流則を適用すると:
\(I_1 + I_3 = I_2 + I_4\) または \(I_1 + I_3 - I_2 - I_4 = 0\)
この式は、節点Aに流れ込む電流と流れ出る電流の総和が等しいことを表しています。
複雑な回路を解析する際は、まずキルヒホッフの法則に基づいて連立方程式を立て、未知の電流や電圧を求めます。また、対称性や回路の特性を利用して方程式を簡略化できる場合もあります。
直列・並列回路
電気回路の基本的な接続方法として、直列接続と並列接続があります。それぞれの接続方法によって、電流・電圧・抵抗の関係が異なります。
- 同じ電流が全ての素子を流れる: \(I = I_1 = I_2 = ... = I_n\)
- 全体の電圧は各素子の電圧の和: \(V = V_1 + V_2 + ... + V_n\)
- 合成抵抗は各抵抗の和: \(R = R_1 + R_2 + ... + R_n\)
- 同じ電圧が全ての素子にかかる: \(V = V_1 = V_2 = ... = V_n\)
- 全体の電流は各素子の電流の和: \(I = I_1 + I_2 + ... + I_n\)
- 合成抵抗の逆数は各抵抗の逆数の和: \(\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + ... + \frac{1}{R_n}\)
- 2つの抵抗の場合: \(R = \frac{R_1 R_2}{R_1 + R_2}\)
例題:抵抗の直列・並列接続
抵抗 \(R_1 = 100 \Omega\) と \(R_2 = 200 \Omega\) があるとき:
直列接続の合成抵抗: \(R = R_1 + R_2 = 100 + 200 = 300 \Omega\)
並列接続の合成抵抗: \(R = \frac{R_1 R_2}{R_1 + R_2} = \frac{100 \times 200}{100 + 200} = \frac{20000}{300} \approx 66.7 \Omega\)
複雑な回路では、直列・並列の組み合わせを見つけて回路を簡略化することが重要です。回路を段階的に簡略化することで、複雑な回路の等価抵抗を求めることができます。
分圧・分流回路
分圧回路と分流回路は、電気回路の基本的な構成で、電圧や電流の分配を扱います。
直列接続された抵抗に電圧をかけると、各抵抗にかかる電圧は抵抗値に比例して分配される。
\[ \begin{aligned} V_i = V \times \frac{R_i}{R_{total}} \\[10pt] \end{aligned} \]
ここで、\(V_i\) は抵抗 \(R_i\) にかかる電圧、\(V\) は全体の電圧、\(R_{total}\) は全抵抗の合計です。
並列接続された抵抗に電流を流すと、各抵抗を流れる電流は抵抗値に反比例して分配される。
\[ \begin{aligned} I_i = I \times \frac{R_{total}/R_i}{\sum_j (R_{total}/R_j)} = I \times \frac{1/R_i}{\sum_j (1/R_j)} \\[10pt] \end{aligned} \]
2つの抵抗の場合は、以下のように簡単になります:
\[ \begin{aligned} I_1 = I \times \frac{R_2}{R_1 + R_2} \\[10pt] I_2 = I \times \frac{R_1}{R_1 + R_2} \\[10pt] \end{aligned} \]
例題:分圧・分流の計算
分圧の例: 100Ωと200Ωの抵抗が直列接続され、全体に30Vの電圧がかかる場合
100Ωの抵抗にかかる電圧: \(V_1 = 30 \times \frac{100}{100+200} = 10\text{ V}\)
200Ωの抵抗にかかる電圧: \(V_2 = 30 \times \frac{200}{100+200} = 20\text{ V}\)
分流の例: 100Ωと200Ωの抵抗が並列接続され、全体に0.3Aの電流が流れる場合
100Ωの抵抗を流れる電流: \(I_1 = 0.3 \times \frac{200}{100+200} = 0.2\text{ A}\)
200Ωの抵抗を流れる電流: \(I_2 = 0.3 \times \frac{100}{100+200} = 0.1\text{ A}\)
分圧・分流の法則は、直列・並列回路における電圧・電流の分配を簡単に計算できる強力なツールです。複雑な回路でも、これらの法則を適用できる部分を見つけることで解析が容易になります。
🔍 ワンポイントアドバイス: 電気回路の解析では、未知数を一つ決めて(この問題では\(I_2\))、他の全ての量をその未知数で表現していく方法が効果的です。キルヒホッフの法則を適用する際は、電流の向きや電圧の極性に注意しましょう。また、計算過程でミスを防ぐために、単位を常に確認し、途中式も丁寧に書き出すことが重要です。複雑な回路でも、基本法則を適用して段階的に解析することで、正確な答えに到達できます。
まずはこの回路がどんな構造になってるか確認するで。図を見てみよか。
この回路は複雑そうに見えるけど、分流・合流の考え方で解けるんや。まず、この回路の構造を説明してみてくれるか?
はい、先生!この回路は、電流源から出た電流I₁がR₁とR₂に分岐し、さらにR₂を通った電流がR₃とR₄+R₅の経路に分岐する構造になっています。
具体的には:
・電流I₁はR₁とR₂に分かれます(分流点①)
・R₂を通った電流は再びR₃と、R₄+R₅の直列回路に分かれます(分流点②)
・R₄+R₅を通る電流がI₂となっています
問題では電流比I₂/I₁を求めることが求められています。
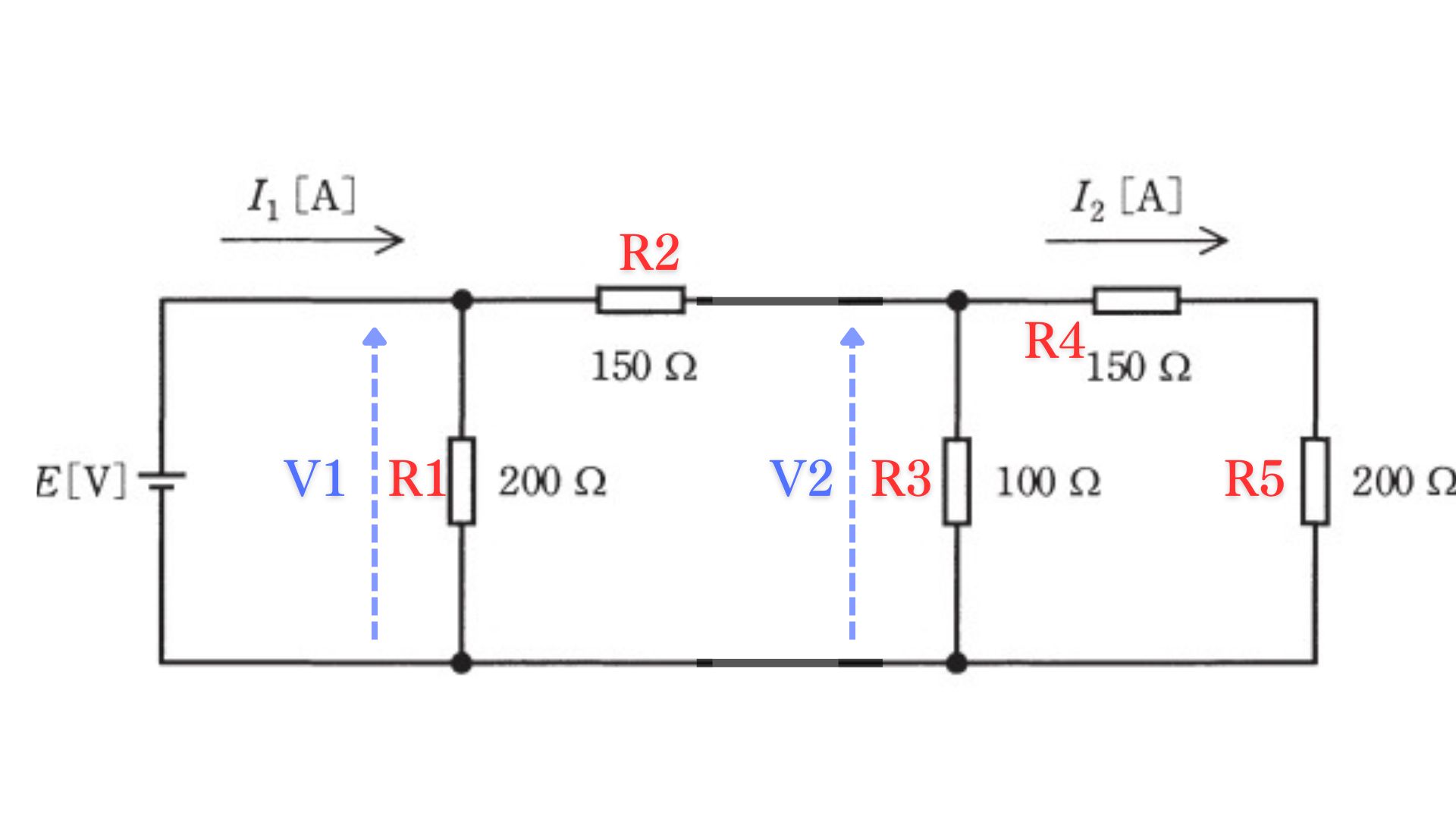
ええやん!じゃあ問題に沿って考えていこか。まずはV₂から計算するんやな。V₂はどこの電圧を表してる?
V₂は図の右側、R₄とR₅の直列回路の両端にかかる電圧です。つまり、電流I₂がR₄とR₅を通過する際に生じる電圧降下の合計を表しています。
そうや!じゃあV₂を計算してみよか。
V₂は電流I₂がR₄とR₅の直列回路を通過する際の電圧降下なので、オームの法則から:
\[ \begin{aligned} V_2 &= (R_4 + R_5) \times I_2 \\ &= (150 + 200) \times I_2 \\ &= 350 \times I_2 \end{aligned} \]よって、V₂ = 350I₂ [V] となります。
ナイス!次に抵抗R₃を流れる電流IR₃を求めるんやけど、どないやって求める?
抵抗R₃を流れる電流IR₃は、V₂をR₃で割ることで求められます。これは、抵抗R₃の両端の電圧がV₂と同じだからです(並列接続のため)。
\[ \begin{aligned} I_{R3} &= \frac{V_2}{R_3} \\ &= \frac{350 \times I_2}{100} \\ &= 3.5 \times I_2 \end{aligned} \]よって、IR₃ = 3.5I₂ [A] となります。
ようできとるな!じゃあR₂を流れる電流IR₂はどないやって求める?キルヒホッフの電流則を使うんやで。
R₂を流れる電流IR₂は、キルヒホッフの電流則(分流点に流入する電流の総和 = 流出する電流の総和)を使って求められます。
分流点②において、R₂から流入する電流IR₂は、R₃に流れる電流IR₃とR₄+R₅に流れる電流I₂に分かれます。
\[ \begin{aligned} I_{R2} &= I_{R3} + I_2 \\ &= 3.5I_2 + I_2 \\ &= 4.5I_2 \end{aligned} \]よって、IR₂ = 4.5I₂ [A] となります。
ええやん!次はV₁を求めるねんけど、V₁はどこの電圧を表してる?
V₁は図の左側、R₁とR₂の並列回路の両端にかかる電圧です。つまり、電流I₁が分岐する分流点①から、IR₃とI₂が合流する点までの電位差を表しています。
そうやな!じゃあV₁を求めるには、どないしたらええやろ?
V₁はV₂とR₂での電圧降下の和として求められます。R₂での電圧降下はオームの法則よりR₂×IR₂です。
\[ \begin{aligned} V_1 &= V_2 + R_2 \times I_{R2} \\ &= 350I_2 + 150 \times 4.5I_2 \\ &= 350I_2 + 675I_2 \\ &= 1025I_2 \end{aligned} \]よって、V₁ = 1025I₂ [V] となります。
計算がとてもうまいな!次はR₁を流れる電流IR₁を求めるけど、どないやって求める?
R₁を流れる電流IR₁は、V₁をR₁で割ることで求められます。これはオームの法則を適用するものです。
\[ \begin{aligned} I_{R1} &= \frac{V_1}{R_1} \\ &= \frac{1025I_2}{200} \\ &= 5.125I_2 \end{aligned} \]よって、IR₁ = 5.125I₂ [A] となります。
すばらしい!最後に求めるI₁はどないやって計算する?
I₁は分流点①において、R₁に流れる電流IR₁とR₂に流れる電流IR₂の和になります。キルヒホッフの電流則より:
\[ \begin{aligned} I_1 &= I_{R1} + I_{R2} \\ &= 5.125I_2 + 4.5I_2 \\ &= 9.625I_2 \end{aligned} \]よって、I₁ = 9.625I₂ [A] となります。
完璧や!最後に求めたい電流比I₂/I₁を計算するで。
電流比I₂/I₁は、I₁ = 9.625I₂の関係を使って計算できます。
\[ \begin{aligned} \frac{I_2}{I_1} &= \frac{I_2}{9.625I_2} \\ &= \frac{1}{9.625} \\ &\approx 0.1 \end{aligned} \]したがって、電流比I₂/I₁は約0.1となります。
よって、選択肢の(1)が正解です。
ようやったな!最後にこの問題で学んだポイントをまとめてみよか。
はい、先生!この問題で学んだ重要なポイントは:
1. 複雑な回路でも、部分に分けて考えれば解けること
2. キルヒホッフの電流則(分流点での電流の保存)が重要
3. 並列接続では電圧が同じ、直列接続では電流が同じという基本原則
4. 電圧降下はオームの法則(V = RI)で計算できること
5. 一つの未知数(ここではI₂)を基準にして他の電流や電圧を表現できること
6. 分流回路では、電流の分配は抵抗値に逆比例するという性質(分流則)
7. 回路解析では、始点から終点に向かって順に解析していくと理解しやすいこと
この問題では、最終的に電流比I₂/I₁ = 0.1を求めることができました。つまり、電流源からの電流I₁のうち、約10%がI₂として流れることがわかりました。
解説まとめ
電源\( V_1 = 60 \ \mathrm{[V]} \)と\( V_2 = 80 \ \mathrm{[V]} \)を個別に考え、重ね合わせの理を使って電流を合算する。
抵抗R_2の並列合成抵抗\( R_2' \)は以下の通り:
\[ \begin{eqnarray} R_2' &=& \frac{R_2 \cdot R_2}{R_2 + R_2} \\[10pt] &=& \frac{R_2}{2} \\[10pt] &=& \frac{60}{2} \\[5pt] &=& 30 \ \mathrm{[\Omega]} \end{eqnarray} \]
この\( R_2' \)とRの直列合成抵抗\( R' \)は:
\[ \begin{eqnarray} R' &=& R + R_2' \\[5pt] &=& 10 + 30 \\[5pt] &=& 40 \ \mathrm{[\Omega]} \end{eqnarray} \]
さらに、\( R' \)とR_1の並列合成抵抗\( R_1' \)は:
\[ \begin{eqnarray} R_1' &=& \frac{R' \cdot R_1}{R' + R_1} \\[5pt] &=& \frac{40 \times 40}{40 + 40} \\[5pt] &=& 20 \ \mathrm{[\Omega]} \end{eqnarray} \]
よって、電源V_1による電流\( I_{\mathrm{v1}} \)は:
\[ \begin{eqnarray} I_{\mathrm{v1}} &=& \frac{V_1}{R_1' + R_1} \\[5pt] &=& \frac{60}{20 + 40} \\[5pt] &=& 1 \ \mathrm{[A]} \end{eqnarray} \]
抵抗Rを流れる電流\( I_1 \)は分流の法則より:
\[ \begin{eqnarray} I_1 &=& \frac{R_1}{R' + R_1} \times I_{\mathrm{v1}} \\[5pt] &=& \frac{40}{40 + 40} \times 1 \\[5pt] &=& 0.5 \ \mathrm{[A]} \end{eqnarray} \]
次に、R_1の並列合成抵抗\( R_1'' \)は:
\[ \begin{eqnarray} R_1'' &=& \frac{R_1 \cdot R_1}{R_1 + R_1} \\[5pt] &=& \frac{R_1}{2} \\[5pt] &=& \frac{40}{2} \\[5pt] &=& 20 \ \mathrm{[\Omega]} \end{eqnarray} \]
この\( R_1'' \)とRの直列合成抵抗\( R'' \)は:
\[ \begin{eqnarray} R'' &=& R + R_1'' \\[5pt] &=& 10 + 20 \\[5pt] &=& 30 \ \mathrm{[\Omega]} \end{eqnarray} \]
これとR_2の並列合成抵抗\( R_2'' \)は:
\[ \begin{eqnarray} R_2'' &=& \frac{R'' \cdot R_2}{R'' + R_2} \\[5pt] &=& \frac{30 \times 60}{30 + 60} \\[5pt] &=& 20 \ \mathrm{[\Omega]} \end{eqnarray} \]
電源V_2による電流\( I_{\mathrm{v2}} \)は:
\[ \begin{eqnarray} I_{\mathrm{v2}} &=& \frac{V_2}{R_2'' + R_2} \\[5pt] &=& \frac{80}{20 + 60} \\[5pt] &=& 1 \ \mathrm{[A]} \end{eqnarray} \]
よって、Rを流れる電流\( I_2 \)は:
\[ \begin{eqnarray} I_2 &=& \frac{R_2}{R'' + R_2} \times I_{\mathrm{v2}} \\[5pt] &=& \frac{60}{30 + 60} \times 1 \\[5pt] &\approx& 0.6667 \ \mathrm{[A]} \end{eqnarray} \]
電流の向きを考慮すると、抵抗Rを流れる合成電流\( I \)は:
\[ \begin{eqnarray} I &=& I_2 - I_1 \\[5pt] &=& 0.6667 - 0.5 \\[5pt] &\approx& 0.1667 \ \mathrm{[A]} \end{eqnarray} \]
したがって、抵抗で消費される電力\( P \)は:
\[ \begin{eqnarray} P &=& R \cdot I^2 \\[5pt] &=& 10 \times 0.1667^2 \\[5pt] &\approx& 0.2779 \rightarrow 0.28 \ \mathrm{[W]} \end{eqnarray} \]